CÁC THUẬT TOÁN SẮP XẾP CƠ BẢN

Khái niệm

Bài toán sắp xếp là bài toán giải quyết việc tổ chức dữ liệu theo một trật tự nhất định, thường là tăng dần hoặc giảm dần.

phép toán cơ bản cho bài toán sắp xếp:

Phép toán đổi chỗ: Là phép toán đảo giá trị 2 biến

 void swap(datatype &a, datatype &b) {
     datatype temp = a; 
     a = b;
     b = temp;
 }

Phép toán so sánh: Trả về true nếu a > b và trả về false cho trường hợp ngược lại.

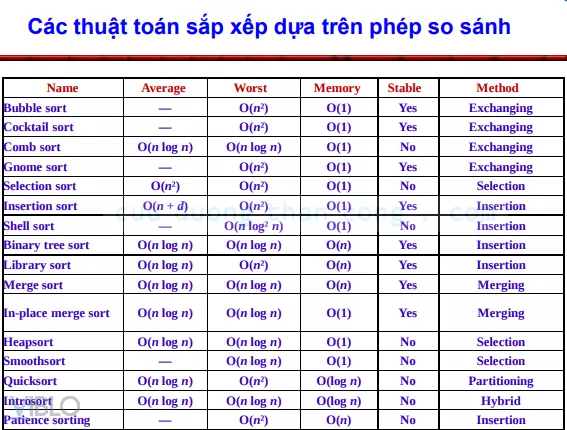
     bool compare(datatype a, datatype b) {
         if (a > b) {
             return true;
         } else {
             return false;
         }
     }

Bảng ghi về độ phức tạp của các thuật toán sắp xếp

Độ phức tạp càng lớn đồng nghĩa với việc thuật toán chạy càng chậm và càng lâu

Ba thuật toán sắp xếp cơ bản

1. Sắp xếp chèn (Insertion Sort)

Ý tưởng: Insertion Sort lấy ý tưởng từ việc chơi bài, dựa theo cách người chơi "chèn" thêm một quân bài mới vào bộ bài đã được sắp xếp trên tay.

Thuật toán:

Tại bước k = 1, 2, ..., n đưa phần tử thứ k trong mảng đã cho vào đúng vị trí trong dãy gồm k phần tử đầu tiên.
Kết quả là sau bước thứ k, sẽ có k phần tử đầu tiên được sắp xếp theo thứ tự.

    void insertionSort(int a[], int array_size) {
        int i, j, last;
        for (i=1; i < array_size; i++) {
            last = a[i];
            j = i;
        while ((j > 0) && (a[j-1] > last)) {
            a[j] = a[j-1];
            j = j - 1; }
            a[j] = last;
        } 
    }

2. Sắp xếp lựa chọn (Selection Sort)

Ý tưởng của Selection sort là tìm từng phần tử cho mỗi vị trí của mảng hoán vị A' cần tìm.

Thuật toán:

Tìm phần tử nhỏ nhất đưa vào vị trí 1
Tìm phần tử nhỏ tiếp theo đưa vào vị trí 2
Tìm phần tử nhỏ tiếp theo đưa vào vị trí 3
...

    void selectionSort(int a[], int n){
        int i, j, min, temp;
        for (i = 0; i < n-1; i++) {
            min = i;
            for (j = i+1; j < n; j++){
                if (a[j] < a[min]) min = j;
            }
            swap(a[i], a[min]);
        }
    }

3. Sắp xếp nổi bọt (Bubble Sort)

Ý tưởng: Bubble Sort, như cái tên của nó, là thuật toán đẩy phần tử lớn nhất xuống cuối dãy, đồng thời những phần tử có giá trị nhỏ hơn sẽ dịch chuyển dần về đầu dãy. Tựa như sự nổi bọt vậy, những phần tử nhẹ hơn sẽ nổi lên trên và ngược lại, những phần tử lớn hơn sẽ chìm xuống dưới.

Thuật toán: Duyệt mảng từ phần tử đầu tiên. Ta sẽ so sánh mỗi phần tử với phần tử liền trước nó, nếu chúng đứng sai vị trí, ta sẽ đổi chỗ chúng cho nhau. Quá trình này sẽ được dừng nếu gặp lần duyệt từ đầu dãy đến cuối dãy mà không phải thực hiện đổi chỗ bất kì 2 phần từ nào (tức là tất cả các phần tử đã được sắp xếp đúng vị trí).

    void bubbleSort(int a[], int n){
        int i, j;
        for (i = (n-1); i >= 0; i--) {
            for (j = 1; j <= i; j++){
                if (a[j-1] > a[j])
                swap(a[j-1],a[j]);
            }
        }
    }

Đánh giá: Tuy đơn giản nhưng Bubble là thuật toán kém hiệu quả nhất trong 3 thuật toán ở mục này

4. So sánh 3 thuật toán

Sắp xếp trộn (Merge Sort)

Sắp xếp trộn (merge sort) là một thuật toán sắp xếp loại so sánh. Thuật toán này là một ví dụ tương đối điển hình của lối thuật toán chia để trị của John von Neumann:

Chia (Divide): Chia dãy gồm n phần tử cần sắp xếp thành 2 dãy, mỗi dãy có n/2 phần tử.
Trị (Conquer): Sắp xếp mỗi dãy con một cách đệ quy sử dụng sắp xếp trộn. Khi dãy chỉ còn một phần tử thì trả lại phần tử này.
Tổ hợp (Combine): Trộn (Merge) hai dãy con được sắp xếp để thu được dãy được sắp xếp gồm tất cả các phần tử của cả hai dãy con.

    MERGE-SORT(A, p, r)
        if p < r 
            then q ← (p + r)/2 // Chia (Divide)
                MERGE-SORT(A, p, q) // Trị (Conquer)
                MERGE-SORT(A, q + 1, r) // Trị (Conquer)
                MERGE(A, p, q, r) // Tổ hợp (Combine)
        endif

    MERGE(M, p, q, r)
        i ← 1; j ← 1
        for k ← p to r do
            if L[ i ] ≤ R[ j ]
            then
                M[k] ← L[ i ]
                i ←i + 1
            else
                M[k] ← R[ j ]
                j ← j + 1

Quick Sort

Quick Sort (QS) được phát triển bởi Hoare năm 1960. Theo thống kê tính toán, QS là thuật toán sắp xếp nhanh nhất hiện nay.

Tương tự như Merge sort, Quick sort là thuật toán sắp xếp được phát triển dựa trên kỹ thuật chia để trị:

Neo đệ qui (Base case). Nếu dãy chỉ còn một phần tử thì nó là dãy đã sắp xếp và trả lại dãy này mà không phải làm gì cả.
Chia (Divide):
- Chọn một phần tử trong dãy và gọi nó là phần tử chốt p (pivot).
- Chia dãy đã cho ra thành hai dãy con: Dãy con trái (L) gồm những phần tử không lớn hơn phần tử chốt, còn dãy con phải (R) gồm các phần tử không nhỏ hơn phần tử chốt. Thao tác này được gọi là thao tác Phân đoạn (Partition).
Trị (Conquer): Lặp lại một cách đệ qui thuật toán đối với hai dãy con L và R.
Tổng hợp (Combine): Dãy được sắp xếp là L p R.

    Quick-Sort(A, Left, Right)
        if (Left < Right ) {
            Pivot = Partition(A, Left, Right);
            Quick-Sort(A, Left, Pivot – 1);
            Quick-Sort(A, Pivot + 1, Right); }

Chọn phần tử chốt:

Việc chọn phần tử chốt nắm vai trò quyết định đối với hiệu năng của thuật toán. Tốt nhất là chọn phần tử chốt là trung vị của danh sách. Tuy nhiên cách này rất khó nên ta có thể chọn phần tử chốt theo những cách sau:

Chọn phần tử đứng đầu hoặc đứng cuối làm phần tử chốt.
Chọn phần tử đứng giữa dãy làm phần tử chốt.
Chọn phần tử trung vị trong 3 phần tử đứng đầu, đứng giữa và đứng cuối làm phần tử chốt.
Chọn phần tử ngẫu nhiên làm phần tử chốt. (Cách này có thể dẫn đến khả năng rơi vào các trường hợp đặc biệt).

Thuật toán Phân đoạn Partition: Mục đích của hàm Partition(A, left, right) là chia A[left..right] thành hai đoạn A[left..pivot –1] và *A[pivot+1..right], sao cho:

A[left..pivot –1] là tập hợp các phần tử có giá trị nhỏ hơn hoặc bằng A[pivot].
A[pivot+1..right] là tập hợp các phần tử có gía trị lớn hơn A[pivot]

Trên đây là một số những thuật toán sắp xếp mình đã tìm hiểu, nếu có gì sai sót, bạn góp ý cho mình tại địa chỉ email nhé. Mình sẽ cập nhật thêm chức năng bình luận trong tương lai để có thể dễ dàng tương tác cùng mọi người hơn

Hi vọng bài viết này có ích với bạn.

90sCode

Tìm kiếm Blog này

Data-Driven Programming